在益智游戏领域,汉诺塔凭借其简洁规则与烧脑机制,成为训练逻辑思维的经典工具。本文将从游戏机制解析、核心策略拆解到效率优化技巧,提供一套完整的通关指南,并结合玩家反馈与未来发展趋势,助你快速掌握这一数学谜题的精髓。
一、游戏核心机制与难点分析
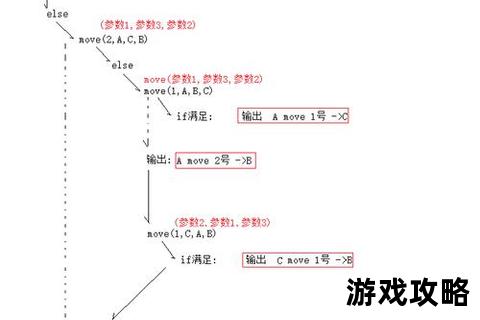
汉诺塔的规则看似简单:通过三根柱子(通常标记为A、B、C),将N个从大到小堆叠的圆盘从起点柱全数移至目标柱,且每次只能移动一个圆盘,且小盘必须在大盘之上。其难点在于:
1. 指数级复杂度:移动次数随层数呈指数增长(公式为 (2^n -1))。例如3层需7步,5层需31步,而8层则需255步。
2. 递归逻辑的抽象性:玩家需通过“中间柱过渡”的思维分解问题,这对新手而言容易陷入步骤混乱。
3. 路径选择的唯一性:每一步移动必须符合目标导向,否则可能导致后续步骤无法衔接。
二、通关策略:从基础到高阶技巧

1. 基础步骤:递归算法的实战应用
递归是解决汉诺塔的核心思想,通过“分解-解决-合并”三步实现:
步骤一:将顶部N-1层从起点柱A移至过渡柱B(借助目标柱C);
步骤二:将第N层(最底层)从A直接移至目标柱C;
步骤三:将N-1层从B移至C(借助A)。
以3层为例:
移动1:A→C
移动2:A→B
移动1:C→B
移动3:A→C
移动1:B→A
移动2:B→C
移动1:A→C
此模式可推广至任意层数,关键在于反复调用递归逻辑。
2. 高效通关:非递归与动态规划优化
对于高阶玩家,非递归方法可减少重复计算:
奇偶分层法:奇数层优先移动最小盘,偶数层按固定顺序循环(如A→B→C→A)。
二进制辅助法:将移动步骤与二进制数对应,通过最低位1的位置确定移动方向。
动态规划记忆:记录已完成的子问题,避免重复操作,尤其适用于超多层数(如在线竞技模式)。
3. 实战口诀与避坑指南
口诀:“小盘先行,隔步动大;奇偶交替,目标导向”。
常见错误:
未预留过渡空间导致路径阻塞;
忽视最小盘的频繁移动规律(每两步需移动一次)。
三、游戏生态:版本选择与安全建议
1. 主流版本与下载渠道
教育版(如Tower of Hanoi Educational):适合新手,内置教程与步数统计,可通过Google Play或App Store官方下载。
竞技版(如Hanoi Tower 3D):支持多人排名与限时挑战,需注意选择认证平台(如九游、TapTap)以避免盗版风险。
2. 安全注意事项
权限管理:拒绝非必要的存储或摄像头访问,尤其警惕第三方平台的无认证应用。
防沉迷设置:部分版本内置时间锁功能,建议开启以平衡娱乐与学习。
四、玩家评价与未来展望
1. 用户反馈
好评点:
“烧脑但成就感极强,尤其破解高难度层数时”;
“递归思维对编程学习有直接帮助”。
争议点:
“纯数学机制缺乏视觉激励,易疲劳”;
“非递归解法教程较少,自学门槛高”。
2. 未来发展趋势
AI辅助教学:结合动态路径提示与错误预判,降低学习曲线。
多场景融合:如将汉诺塔规则融入剧情解谜或团队协作模式,提升趣味性。
跨学科应用:优化算法在云计算任务调度、机器人路径规划等领域的实践。
汉诺塔不仅是考验耐心的智力游戏,更是训练抽象思维与递归逻辑的绝佳工具。通过掌握核心策略、合理选择版本并关注安全规范,玩家可逐步从新手进阶为通关高手。未来,随着技术融合与玩法创新,这一经典谜题或将焕发全新生命力。

